Rounding shootouts - Year 3-6 (Year 3-4 whole numbers, Year 5-6 decimals)
- Chris Weedon
- Jul 19, 2024
- 2 min read
Story: Did you know shooting is an Olympic event? Well, maybe we will use nerf guns just in case...(for extreme student engagement, use a single nerf gun and invite volunteers to 'shoot' at rounded numbers written on the whiteboard, rolling dice or using Google's random number generate to create a number that needs to be rounded each time).
Tools: Playing cards and maths grid books. Nerf gun or water gun for the hook, 'shooting' at the whiteboard for whole-class modelling.
Main event
Set up a shooting target list - these are the little clay targets that float into the air and need to be shot to the ground.
You are lucky - your gun is actually pretty forgiving, so even if you get pretty close, the clay target shatters from the passing shot's momentum. So, you don't have to hit the exact number, you just have to be close - your shot has to round to that target.
Pull cards.
Arrange these to form a number.
Aim to round that number to a target that you still need to score, writing the arranged number beside the target number.
Complete each target number on you list, before your opponent completes theirs.
Record as you go.
If you cannot arrange the cards to score a target that is left on your board, that is a missed turn - better luck next time you pull cards.
First to complete their board, shooting down all targets with rounded shots, wins!
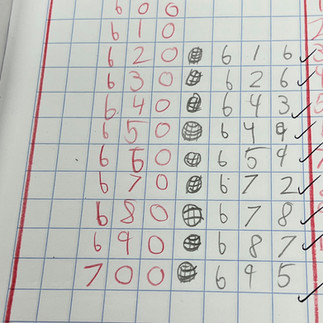
Extension 1: Set up 3-digits, or rounding to tens targets within 4-digit numbers, or decimal targets. See the examples in the photos - this is a very flexible game depending on how you set up the initial rounding board.
For decimals, just use a counter alongside the playing cards to represent the decimal point.
Extension 2: Set up a gameboard of 10 fractions. For example, 1/4, 5/6, 2/3, and 7 more fractions. Roll two dice or pull two cards - whoever can make a fraction closest to one on their rounding gameboard, ticks it off and writes the fraction created beside it. BUT the fraction cannot be identical - you cannot tick off 1/4 with 1/4. But you can tick off 1/4 with 2/8, or even a fraction that is not equivalent, if it is closer to the fraction on your board compared to your partner's board.







































Comments